Praticamente, todo livro de machine learning trata da apresentação do dilema do bias-variância e utiliza sua inerente decomposição na discussão das técnicas de validação cruzada e sintonia de hiperparâmetros.
Para além da fundamentação téorica, apresento neste post e no próximo post um framework básico para decomposição do bias, variância e do erro irredutível independente do modelo preditivo utilizado - Ao final chegaremos aos famosos gráficos de decomposição do bias-variance apresentados nos livros, mas que comumente não possuem explicação quanto sua construção.
Revisão de estatística
Dois conceitos são chave na teória de probabilidades e no desenvolvimento do dilema do bias-variância são a esperança matemática (valor esperado) e a variância.
A esperança estatística é definida matemáticamente como a integral em todo intervalo real do produto da variável aleatória $x$ pela sua probabilidade de ocorrência.
\[E[X]=\int_{-\infty}^\infty x f(x)dx\]Tratando-se de uma variável $x$ discreta, a integral assume a forma de um somátorio.
\[E[X]=\sum_{i=1}^{\infty} x_i p(x_i)\]A análise da equação acima nos permite identificar que a esperança de uma variável discreta corresponde a sua média aritmética, uma vez que $p(x)$ pode ser expresso como a razão entre o número de observações de um determinado $x_i$ e o número total de observações.
A variância é definida matematicamente como a esperança do quadrado da diferença entre a variável e seu valor esperado.
\[Var(X) = E\left [ \left ( X - E\left ( X \right ) \right )^2 \right ]\]A expansão dos termos da equação acima, nos leva a seguinte expressão:
\[Var(X) = E\left [ \left ( X^2 - 2 \cdot X \cdot E\left ( X \right ) + \left ( E\left ( X \right ) \right )^2 \right ) \right ]\]E ao aplicarmos o operador esperança no polinômio acima e utilizando a sua propriedade cumulativa chegamos a seguinte expressão:
\[Var(X) = E\left ( X^2 \right ) - 2 \cdot E\left (X \cdot E\left ( X \right ) \right ) + E\left ( E\left ( X \right ) \right )^2\]Sendo a esperança de uma variável X uma constante, a esperança dela equivalente à própria.
\[Var(X) = E\left ( X^2 \right ) - 2 \cdot \left (E\left ( X \right ) \right )^2 + \left ( E\left ( X \right ) \right )^2 = E\left ( X^2 \right ) - \left ( E\left ( X \right ) \right )^2\]Para facilitar a decomposição do bias-variância que veremos a seguir, vamos organizar a equação acima da seguinte forma:
\[E\left ( X^2 \right ) = Var(X) + \left ( E\left ( X \right ) \right )^2\]Decomposição do erro esperado
Dada uma variável $y^*$ cuja predição é desejada, iremos assumir a existência de um modelo idealizado $f(x)$ capaz de explicar integralmente o comportamento desta variável.
\[y^* = f(x)\]Na prática, $y^*$ está sujeita à sua própria variabilidade, de forma que expandimos a equação acima para a forma:
\[y = f(x) + \sigma_y\]Apesar de desconhecermos $f(x)$, é possível predizer os valores de $y$ através de modelos matemáticos empirícos baseados em dados, o qual denominaremos $\widehat{f}(x)$. O objetivo de toda modelagem é obter uma função $\widehat{f}(x)$ cujos valores preditos sejam os mais próximos possíveis de $y$ para um dado vetor de preditores $x = [x_1, x_2, … x_p]$.
Vamos supor que para medir o quão “próximo” são os valores de $y$ e $\widehat{f}(x_0)$ utilizaremos uma medida quadrática tal como o erro quadrático, isto é $(y - \widehat{f}(x_0))^2$, neste caso, nosso erro esperado. Observe que estamos avaliando a função em um único ponto $x_0$.
É fato que para cada conjunto de dados utilizado obteremos um diferente valor de $\widehat{f}(x_0)$ e, de forma equivalente, um diferente valor de $y$. Para compensar essa variabilidade e obter um valor representativo podemos trabalhar com a esperança estatística da quantidade quadrática que estamos avaliando.
\[E(\epsilon) = E((y - \widehat{f}(x_0))^2)\]Expandindo a quantidade acima, chegamos a seguinte expressão:
\[E((y - \widehat{f}(x_0))^2) = E(y^2 + (\widehat{f}(x_0))^2 - 2 \cdot y \cdot \widehat{f}(x_0))\] \[E((y - \widehat{f}(x_0))^2) = E(y^2) + E(\widehat{f}(x_0))^2) - 2 \cdot E(y \cdot \widehat{f}(x_0))\]Utilizando a transformação quanto a variância apresentada na seção 1, podemos expandir os termos com a esperança da variável ao quadrado para a forma:
\[E((y - \widehat{f}(x_0))^2) = Var(y) + (E(y))^2 + Var(\widehat{f}(x_0))) + (E(\widehat{f}(x_0)))^2 - 2 \cdot E(y \cdot \widehat{f}(x_0))\]Rearranjamos os termos para fins de praticidade dos próximos passos:
\[E((y - \widehat{f}(x_0))^2) = Var(y) + Var(\widehat{f}(x_0))) + [(E(y))^2 + (E(\widehat{f}(x_0)))^2 - 2 \cdot E(y \cdot \widehat{f}(x_0))]\]A expressão acima pode ter seu último termo simplificado pelo conceito de produto notável para a forma:
\[E((y - \widehat{f}(x_0))^2) = Var(y) + Var(\widehat{f}(x_0)) + [E(y) - E(\widehat{f}(x_0))]^2\]Dado que $y = f(x) + \sigma_y$, a esperança de $y$ - $E(y)$ - é igual ao próprio $f(x)$ visto que se espera que a esperança, o valor médio, de $\sigma_y$ - $E(\sigma_y)$ - seja igual a zero. Por outro lado, a variância de $y$ - $Var(y)$ é igual ao próprio $\sigma_y$, uma vez que se espera que $f(x)$ tenha variância nula por ser o modelo idealizado. Desta forma, o erro esperado toma a seguinte expressão:
\[E((y - \widehat{f}(x_0))^2) = \sigma_y + Var(\widehat{f}(x_0)) + [f(x) - E(\widehat{f}(x_0))]^2\]A expressão acima é o que a literatura indica como a decomposição em bias-variância do erro esperado.
\[E((y - \widehat{f}(x_0))^2) = Erro_{irredutível} + Variância + (Bias)^2\]Interpretação dos termos da decomposição
O bias - $[f(x) - E(\widehat{f}(x_0)]$ - corresponde ao grau de próximidade do modelo proposto ao modelo ideal - $f(x)$. Observe, contudo, que não tratamos diretamente do modelo proposto $\widehat{f}(x_0)$, mas da esperança (média) de modelos propostos - $E(\widehat{f}(x_0))$.
E o que é a esperança de um modelo?
O termo $E(\widehat{f}(x_0))$ corresponde ao valor médio de diferentes modelos $f(x)$ aplicados no ponto $x_0$.
Por esta razão que o bias-variância é simulado.
Na prática teremos um único banco de dados, obteremos um determinado $\widehat{f}(x)$ e teremos uma estimativa do erro esperado.
Não é possível decompor o erro esperado em termos do bias e da variância com um único modelo construido. Por esta razão, simulamos diferentes bancos de dados para a construção de diferentes modelos e a obtenção de diferentes estimativas pontuais.
A diferença entre o valor do modelo perfeito em um ponto $x_0$ e o valor médio de diferentes modelos $\widehat{f}(x)$ no mesmo ponto é o que matemáticamente denomina-se como bias.
E a variância?
A variância segue o mesmo princípio, sua estimativa passa pela construção de diferentes modelos vindo de diferentes bancos de dados, a aplicação destes modelos em um ponto $x_0$ e então a estimativa da variância para cada valor de $\widehat{f}(x_0)$.
O último termo de nossa equação - erro irredutível - é a própria variabilidade de $y$ e nos fornece uma importante conclusão: Nenhum modelo pode ter erro esperado menor que a variabilidade da variável predita.
Tá… e o onde está o tradeoff?
Certo! Até agora, verificamos como decompor o erro esperado nas suas parcelas de bias, variância e erro irredutível. Para enxergar o dilema (tradeoff) existente, passemos para um exemplo intuitivo!
Noção intuitiva do dilema do bias-variância
Digamos que possuimos o conjunto de dados apresentado na figura a seguir. Nossa variável de interesse $Y$ é uma função linear da preditora $x$.
set.seed(42)
cars %>%
filter(dist < 80) %>%
group_by(speed) %>%
summarise(dist = mean(dist)) %>%
sample_n(10) %>%
ggplot(aes(x = speed, y = dist)) +
geom_point() + labs(x = "x", y = "y") +
theme(axis.text = element_text(family = "serif", face = "bold", size = 12))
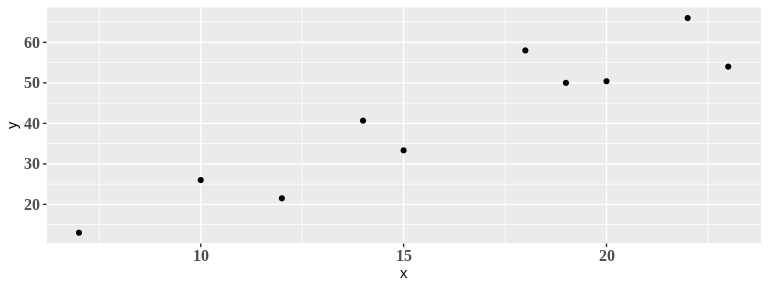
Podemos a partir do conjunto de dados acima propor diferentes modelos polinomiais, digamos que ajustaremos os modelos de primeira ordem (linear), terceira ordem e quinta ordem e nona ordem. O perfil de cada um destes modelos é apresentado a seguir.
set.seed(42)
plot1 <- cars %>%
filter(dist < 80) %>%
group_by(speed) %>%
summarise(dist = mean(dist)) %>%
sample_n(10) %>%
ggplot(aes(x = speed, y = dist)) +
geom_point() + labs(x = "x", y = "y") +
theme(axis.text = element_text(family = "serif", face = "bold", size = 12)) +
stat_smooth(aes(x = speed, y = dist), method = "lm",na.rm = TRUE,
formula = y ~ poly(x, 1), se = FALSE) + xlim(0, 25) + ylim(0,70)
set.seed(42)
plot2 <- cars %>%
filter(dist < 80) %>%
group_by(speed) %>%
summarise(dist = mean(dist)) %>%
sample_n(10) %>%
ggplot(aes(x = speed, y = dist)) +
geom_point() + labs(x = "x", y = "y") +
theme(axis.text = element_text(family = "serif", face = "bold", size = 12)) +
stat_smooth(aes(x = speed, y = dist), method = "lm",na.rm = TRUE,
formula = y ~ poly(x, 3), se = FALSE) + xlim(0, 25) + ylim(0,70)
set.seed(42)
plot3 <- cars %>%
filter(dist < 80) %>%
group_by(speed) %>%
summarise(dist = mean(dist)) %>%
sample_n(10) %>%
ggplot(aes(x = speed, y = dist)) +
geom_point() + labs(x = "x", y = "y") +
theme(axis.text = element_text(family = "serif", face = "bold", size = 12)) +
stat_smooth(aes(x = speed, y = dist), method = "lm",na.rm = TRUE,
formula = y ~ poly(x, 5), se = FALSE) + xlim(0, 25) + ylim(0,70)
set.seed(42)
plot4 <- cars %>%
filter(dist < 80) %>%
group_by(speed) %>%
summarise(dist = mean(dist)) %>%
sample_n(10) %>%
ggplot(aes(x = speed, y = dist)) +
geom_point() + labs(x = "x", y = "y") +
theme(axis.text = element_text(family = "serif", face = "bold", size = 12)) +
stat_smooth(aes(x = speed, y = dist), method = "lm",na.rm = TRUE,
formula = y ~ poly(x, 7), se = FALSE) + xlim(0, 25) + ylim(0,70)
grid.arrange(plot1, plot2, plot3, plot4, ncol=2)
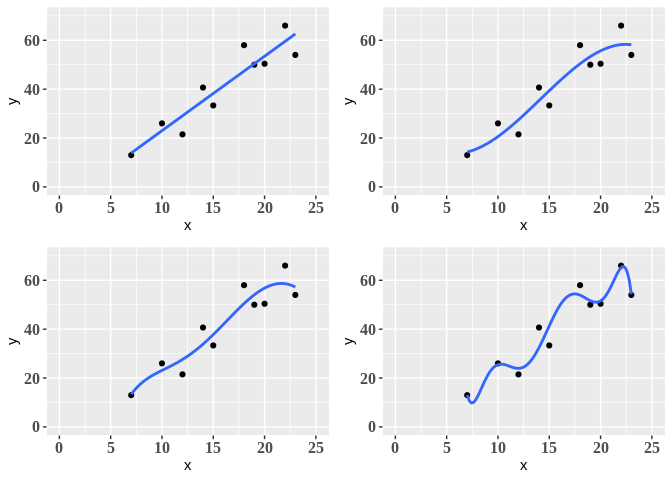
Analisando os gráficos acima vemos que conforme aumentamos o grau do polinômio, ou seja, a complexidade do modelo, obtemos uma curva mais aderente aos dados - dizemos, desta forma, que conforme aumentamos a complexidade do modelo, reduzimos o bias associado ao modelo.
Esta observação se torna mais clara, se ao invés de poucos pontos, povoassemos todo o espaço da variável preditora. Neste caso, apesar do último modelo ser de grau 7, seu comportamento seria equivalente ao de uma reta, portanto, se aproximando do modelo ideal linear.
set.seed(42)
dc <- cars %>%
filter(dist < 80) %>%
group_by(speed) %>%
summarise(dist = mean(dist)) %>%
sample_n(10)
lm(dist ~ speed, data = dc) %>%
predict(data.frame(speed = seq(0,25,0.01))) %>%
as_tibble() %>%
rename(dist = value) %>%
mutate(dist = dist + rnorm(length(seq(0,25,0.01))),0,0.2) %>%
mutate(speed = seq(0,25,0.01)) %>%
filter(dist > 0) %>%
ggplot(aes(x = speed, y = dist)) +
geom_point() + labs(x = "x", y = "y") +
theme(axis.text = element_text(family = "serif", face = "bold", size = 12)) +
stat_smooth(aes(x = speed, y = dist), method = "lm",na.rm = TRUE,
formula = y ~ poly(x, 7), se = FALSE) + xlim(0, 25) + ylim(0,70)
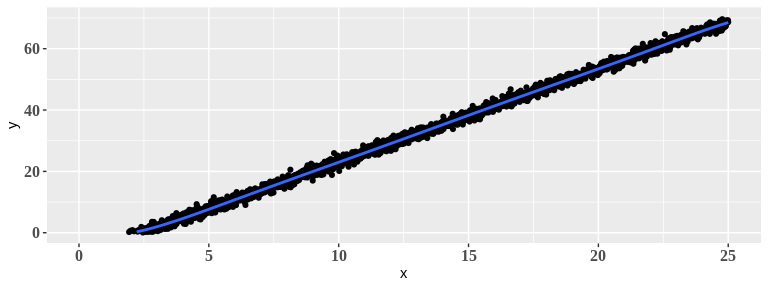
Experimentemos agora, gerar outros dados vindo do mesmo banco de dados cars e observar o comportamento dos modelos polinomiais - alteremos para set.seed(43) no código anterior.
set.seed(43)
plot1 <- cars %>%
filter(dist < 80) %>%
group_by(speed) %>%
summarise(dist = mean(dist)) %>%
sample_n(10) %>%
ggplot(aes(x = speed, y = dist)) +
geom_point() + labs(x = "x", y = "y") +
theme(axis.text = element_text(family = "serif", face = "bold", size = 12)) +
stat_smooth(aes(x = speed, y = dist), method = "lm",na.rm = TRUE,
formula = y ~ poly(x, 1), se = FALSE) + xlim(0, 25) + ylim(0,70)
set.seed(43)
plot2 <- cars %>%
filter(dist < 80) %>%
group_by(speed) %>%
summarise(dist = mean(dist)) %>%
sample_n(10) %>%
ggplot(aes(x = speed, y = dist)) +
geom_point() + labs(x = "x", y = "y") +
theme(axis.text = element_text(family = "serif", face = "bold", size = 12)) +
stat_smooth(aes(x = speed, y = dist), method = "lm",na.rm = TRUE,
formula = y ~ poly(x, 3), se = FALSE) + xlim(0, 25) + ylim(0,70)
set.seed(43)
plot3 <- cars %>%
filter(dist < 80) %>%
group_by(speed) %>%
summarise(dist = mean(dist)) %>%
sample_n(10) %>%
ggplot(aes(x = speed, y = dist)) +
geom_point() + labs(x = "x", y = "y") +
theme(axis.text = element_text(family = "serif", face = "bold", size = 12)) +
stat_smooth(aes(x = speed, y = dist), method = "lm",na.rm = TRUE,
formula = y ~ poly(x, 5), se = FALSE) + xlim(0, 25) + ylim(0,70)
set.seed(43)
plot4 <- cars %>%
filter(dist < 80) %>%
group_by(speed) %>%
summarise(dist = mean(dist)) %>%
sample_n(10) %>%
ggplot(aes(x = speed, y = dist)) +
geom_point() + labs(x = "x", y = "y") +
theme(axis.text = element_text(family = "serif", face = "bold", size = 12)) +
stat_smooth(aes(x = speed, y = dist), method = "lm",na.rm = TRUE,
formula = y ~ poly(x, 7), se = FALSE) + xlim(0, 25) + ylim(0,70)
grid.arrange(plot1, plot2, plot3, plot4, ncol=2)
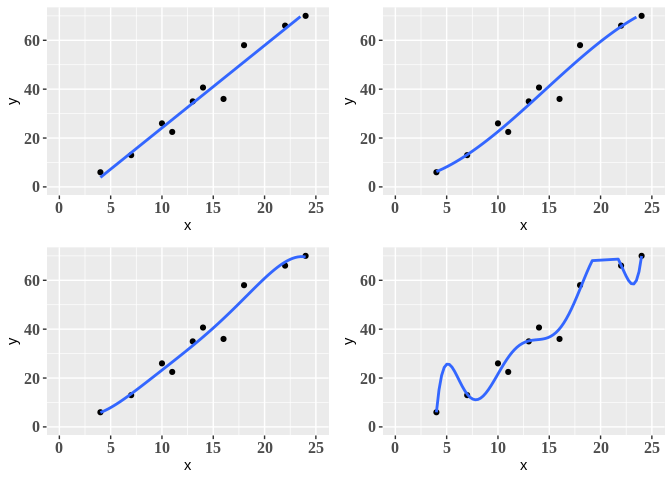
Compare o gráfico acima com o gerado anteriormente.
Observe que conforme se aumenta o grau do polinômio (complexidade do modelo) menos o modelo ajustado é similar ao equivalente na primeira figura - dizemos, neste caso, que a variância entre os modelo aumenta conforme a complexidade.
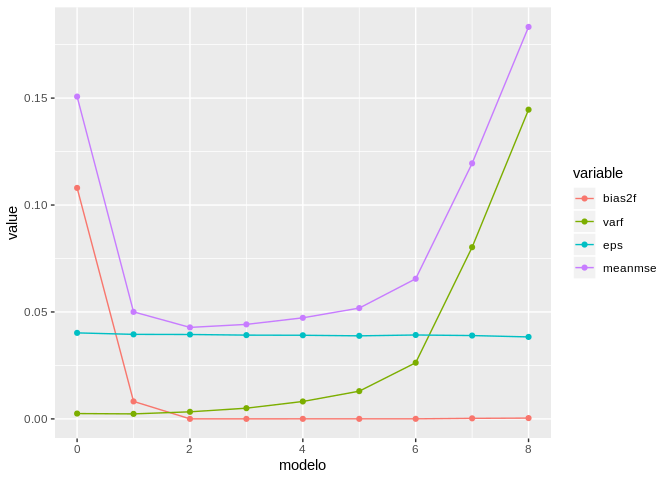
Com base nesta abordagem intuitiva fica claro que o bias reduz com a complexidade do modelo e o inverso ocorre com a variância. O erro irredutível é constante, e o erro esperado corresponde a soma destes três últimos termos. Estes fatos podem ser resumidos na figura a seguir, resultado de uma simulação de bias-variância que abordaremos no próximo post.
Edit: O gráfico abaixo é gerado pelo código a seguir! Bons estudos galera!
# Carregamento de pacotes do R
library(tidyverse)
library(magrittr)
# Controle da seed do número aleatório para garantir reprodutibilidade dos resultados
set.seed(42)
# Criação do modelo perfeito
fun <- function(x) x^2
# Definição do dominio de avaliação do bias-variance
ref <- tibble(x = seq(0,1,0.1)) %>%
mutate(y = fun(x))
# Criação de uma função para simular uma amostragem real
# - 50 observações
# - Dentro do dominio de x (0 a 1)
data_sim <- function(n = 50){
x = runif(n = n, min = 0, max = 1)
y = fun(x) + rnorm(n = n, mean = 0, sd = 0.2)
data = tibble::tibble(x, y)
return(data)
}
# Objeto para armazenar os resultados do que vem a seguir
dados = data.frame(modelo = NA, x = NA, y = NA, pred = NA)
# Construção e predição de 500 moddelos de diferentes graus polinomiais
# Cada modelo recebe o mesmo conjunto de dados por i-teração
# A cada i-teração o conjunto de dados é alterado pela função 'data_sim()'
for (i in 1:500) {
sim <- data_sim()
model0 <- lm(y ~ 1, data = sim) %>%
predict(select(ref, x))
model1 <- lm(y ~ poly(x, degree = 1), data = sim) %>%
predict(select(ref, x))
model2 <- lm(y ~ poly(x, degree = 2), data = sim) %>%
predict(select(ref, x))
model3 <- lm(y ~ poly(x, degree = 3), data = sim) %>%
predict(select(ref, x))
model4 <- lm(y ~ poly(x, degree = 4), data = sim) %>%
predict(select(ref, x))
model5 <- lm(y ~ poly(x, degree = 5), data = sim) %>%
predict(select(ref, x))
model6 <- lm(y ~ poly(x, degree = 6), data = sim) %>%
predict(select(ref, x))
model7 <- lm(y ~ poly(x, degree = 7), data = sim) %>%
predict(select(ref, x))
model8 <- lm(y ~ poly(x, degree = 8), data = sim) %>%
predict(select(ref, x))
# Geração de um ruído branco para adição aos resultados preditos pelos modelos
eps <- rnorm(n = 11, mean = 0, sd = 0.2)
# Armazenamento dos resultados e adição do ruido branco criado acima
dados %<>%
rbind(data.frame(modelo = 0, x = select(ref, x),
select(ref, y)+eps, pred = model0)) %>%
rbind(data.frame(modelo = 1, x = select(ref, x),
select(ref, y)+eps, pred = model1)) %>%
rbind(data.frame(modelo = 2, x = select(ref, x),
select(ref, y)+eps, pred = model2)) %>%
rbind(data.frame(modelo = 3, x = select(ref, x),
select(ref, y)+eps, pred = model3)) %>%
rbind(data.frame(modelo = 4, x = select(ref, x),
select(ref, y)+eps, pred = model4)) %>%
rbind(data.frame(modelo = 5, x = select(ref, x),
select(ref, y)+eps, pred = model5)) %>%
rbind(data.frame(modelo = 6, x = select(ref, x),
select(ref, y)+eps, pred = model6)) %>%
rbind(data.frame(modelo = 7, x = select(ref, x),
select(ref, y)+eps, pred = model7)) %>%
rbind(data.frame(modelo = 8, x = select(ref, x),
select(ref, y)+eps, pred = model8))
}
# Apresentação dos resultados
dados %<>% as.tibble() %>% na.omit()
# Variância em função da ordem do modelo
var <- dados %>%
group_by(modelo, x) %>%
summarise(varfx = var(pred)) %>%
group_by(modelo) %>%
summarise(varf = mean(varfx))
# Bias em função da ordem do modelo
bias <- dados %>%
group_by(modelo, x) %>%
summarise(meanf = mean(pred)) %>%
mutate(bias2 = (meanf - fun(x))^2) %>%
group_by(modelo) %>%
summarise(bias2f = mean(bias2))
# Erro médio em função da ordem do modelo
mse <- dados %>%
group_by(modelo, x) %>%
mutate(error = (pred - y)^2) %>%
group_by(modelo) %>%
summarise(meanmse = mean(error))
# Combinação dos resultados
resume <- bias %>%
bind_cols(var %>% select(varf)) %>%
bind_cols(mse %>% select(meanmse)) %>%
mutate(eps = meanmse - bias2f - varf) %>%
select(modelo, bias2f, varf, eps, meanmse)
# Geração do gráfico
resume %>%
reshape2::melt(id.var = "modelo") %>%
ggplot(aes(x = modelo, y = value, col = variable)) +
geom_line() + geom_point()